• Philosophie de l'éducation, aide à l'apprentissage
• Articles du CERFOP

• Recherches psychopédagogiques
• Stratégies d'apprentissage dans l'accès à l'opératoire formel. Étude d'un cas
• La structuration des activités d'apprentissage en pédagogie d'aide (1/2)
• La structuration des activités d'apprentissage en pédagogie d'aide (2/2)

Accueil>Philosophie de l'éducation>Recherches psychopédagogiques

AVANT-PROPOS.

La notion de déficience intellectuelle légère se trouve au coeur d'imprécisions dont la pédagogie de l'éducation spécialisée peut tirer profit. D'une part, les textes qui régissaient les S.E.S[1] désignaient leur population comme relevant des "débiles légers", au Q.I. compris entre 65 et 80[2]. Nous pouvons déjà souligner une non-correspondance avec le recrutement privilégié des S.E.S, censé être les classes de perfectionnement, puisque ces dernières accueillent en principe (arrêté du 12/8/64) les enfants ayant un Q.I. compris entre 50 et 75. Lorsque l'on sait qu'en 1984/85, 43% des élèves de S.E.S provenaient des classes de perfectionnement, il y a déjà là matière à s'interroger. D'autre part, cette même débilité légère, ou, dans une terminologie plus récente, la déficience intellectuelle légère n'est pas sans nous poser d'autres questions. On pouvait déjà s'étonner, en 1988, de la non-concordance entre la classification française (situant la débilité moyenne entre 50 et 65, et la débilité légère entre 65 et 80), et la nomenclature de l'O.M.S qui définit le retard mental moyen comme un Q.I. compris entre 35 et 50, et le retard mental léger entre 50 et 70. Cette classification de l'O.M.S (Cf. Gibello, L'enfant à l'intelligence troublée, 1984) situe hors pathologie les Q.I compris entre 68 et 80, soit la majorité de la population des S.E.S : "Cette catégorie est maintenant considérée comme une variante de la normalité, et cela à très juste titre, puisque les sujets en présentant les caractéristiques psychométriques ne sont pas distinguables de leurs contemporains une fois devenus adultes, et de leur singularité réside dans leur difficulté à suivre la scolarité au rythme de leurs camarades"[3]. Donc, dans la mesure où cette évolution des normes de l'O.M.S est maintenant prise en compte par le Ministère de l'Education Nationale[4], dans la mesure où la désignation des instituteurs de l'option F du C.A.P.S.A.I.S[5] les engage à prendre en charge les "adolescents en difficulté" et non plus seulement les D.I.L., nous sommes à même de nous demander, à la suite de J.L. Moracchini "Les enfants de S.E.S sont-ils toujours débiles"[6] ?

Si les élèves de S.E.S et d'E.R.E.A appartiennent simplement à une variante de la normalité, il est clair que la pédagogie spécialisée - si tant est qu'il existe une pédagogie spécialisée, différente de ce que devrait être toute autre pédagogie - qui doit leur être appliquée, n'est plus contrainte de subordonner sa pratique aux théories psychologiques. Elle pourrait, tout en continuant à s'informer utilement auprès des psychologues, construire un discours autonome. C'est ce que nous essaierons de démontrer, dans la deuxième partie de notre intervention, avant de présenter, dans une troisième partie, le profil des psychologies cognitives. Les directives[7], attribuant aux "sections d'enseignement général et professionnel adapté" l'exigence d'une formation qualifiante de niveau cinq, renforcent notre opinion dans cette voie. Néanmoins, c'est toujours à la psychologie que la pédagogie emprunte les nouveaux concepts lui permettant de structurer sa réflexion et de rectifier sa pratique. Nous montrerons, dans notre première partie, que la naissance des notions de parcours et de stratégie engage déjà un renversement des rapports entre pédagogie et psychologie. C'est à Piaget que nous ferons alors appel, puisque la maîtrise de l'opératoire formel, dernier stade piagétien de l'évolution intellectuelle, semble être la difficulté majeure des D.I.L.

LA DIFFICULTÉ PIAGÉTIENNE : DU CONCRET AU FORMEL.

Rappels.

Avant d'aborder la présentation du groupe (au sens mathématique) I.N.R.C qui définit l'opératoire formel, puis la critique de son application en relation à l'adolescent, nous effectuerons un rapide rappel des stades piagétiens. Il y a trois grande périodes, le sensori-moteur, l'opératoire concret et l'opératoire formel, qui s'échelonnent pour la première de 0 à 2 ans, pour la seconde de 2 à 11 ans, puis de 11/12 à 16 ans pour l'opératoire formel; rappelons encore que l'opératoire concret se divise en une période pré-opératoire (2-7 ans) et en opératoire concret proprement dit (7-11 ans). La relative précision de ces âges ne doit pas nous faire oublier qu'il faut ici prendre avant tout en compte la progression, la succession de ces stades ; Piaget nous mettait lui-même en garde contre une interprétation fixiste de ce découpage : "De là à admettre des stades rigides caractérisés par des limites d'âge constantes et par un contenu permanent de pensée, il y a loin [...] les âges caractéristiques que l'on obtient, même en procédant sur un grand nombre d'enfants, ne sont que des moyennes ; leur succession, quoique réelle globalement, n'exclut donc ni les chevauchements, ni même les régressions individuelles momentanées."[8]. Comme nous le préciserons dans notre troisième partie, une interprétation fixiste - entendons par là un usage des stades piagétiens qui consisterait, après avoir repéré le niveau d'un enfant, à ne pas tenter de le hisser au niveau supérieur - constituerait une aberration pédagogique, le propre de l'action pédagogique étant d'amener l'élève à résoudre des problèmes nouveaux. Il reste que ces stades sont marqués par de nettes différences quant aux capacités de réponse des enfants. Piaget, prônant la continuité du développement de l'enfant, ne cessera de marquer des discontinuités dans la capacité de ce dernier à résoudre les problèmes. Ainsi, la première grande rupture (nous ne prendrons pas en compte ici le passage du sensori-moteur au pré-opératoire), l'accès à l'opératoire concret, est marquée par la maîtrise, vers 7 ou 8 ans, de la réversibilité. La réversibilité est ce qui définit l'opératoire, l'opération étant : "une action intériorisée qui devient réversible et qui se coordonne avec d'autres en structures opératoires d'ensemble."[9]. La réversibilité est bien ici la notion fondamentale ; c'est parce que les opérations sont réversibles qu'elles peuvent se coordonner entre elles, c'est à dire, rapidement : parce que je conçois l'addition de manière réversible, je peux, après avoir ajouté 2 à 4, retirer 2 de 6 ; l'addition et la soustraction sont ainsi dites coordonnées.

Qu'est-ce donc que cette fameuse réversibilité ? Une des principales expériences, bien connues, consiste à mettre l'enfant face à deux verres, l'un bas et large, l'autre mince et haut. On verse, devant l'enfant, le contenu du verre large et bas dans le verre (vide) haut et mince, puis l'on demande : où y a-t-il le plus à boire? Avant l'accès à l'opératoire, l'enfant désignera le verre haut et mince. Après l'accès à l'opératoire et la compréhension que l'action "verser le contenu de A dans B" peut être annulée par l'action inverse et équivalente, "verser le contenu de B dans A", la réponse, immédiate, affirme qu'il y a évidemment la même quantité à boire dans les deux verres. Entre temps, il y a eu constitution d'un "invariant", qui est ici la substance, c'est à dire, chez Piaget, la quantité de matière. La constitution des invariants - dans l'ordre piagétien, critiqué à l'aide de dispositifs expérimentaux différents - commence par la substance puis se poursuit avec le poids et le volume. D'autres exemples du défaut de réversibilité ont des incidences fâcheuses ; ainsi, "...une ligne droite une fois brisée représente un plus long chemin... la distance entre A et B n'est pas nécessairement la même qu'entre B et A (surtout en pente)..."[10]. Il y a, dans ce dernier exemple, une influence persistante de l'égocentrisme (c'est à dire, en termes de psychologie, de l'indistinction du moi et du monde) sur la représentation, l'enfant ne pouvant se représenter la pente sans se voir entrain de la remonter. De même, face à une sériation à trois termes, p. ex. A < B < C , il est très difficile d'admettre que B est en même temps plus grand que A et plus petit que C, et cela parce que la relation "plus grand que", n'ayant pas été comprise de manière réversible, ne peut être coordonnée avec la relation "plus petit que". Une dernière remarque sur cet accès à la réversibilité opératoire : il ne faudrait pas la comprendre, ainsi que le souligne Danset[11], à la suite de Piaget[12], comme une "renversabilité", au sens où, si l'on reversait à nouveau le contenu du verre B dans le verre A, la quantité à boire redeviendrait la même. Il n'y aurait pas alors acquisition d'un invariant, mais imagination d'une double variation. Il y a bien, par la constitution d'un invariant, structuration de la représentation, et si la qualification de concret fait référence à la nécessité d'une manipulation, il ne faudrait donc pas en conclure qu'à ce stade, tout se passe sur le plan pratique.

De même que cet opératoire concret n'est pas seulement concret, l'opératoire formel n'est pas seulement formel mais désigne une refonte systématique de la pensée opératoire. Il pourrait cependant apparaître, d'après certaines descriptions de Piaget, comme ne relevant que de la pensée pure ; l'opératoire formel ne permet-il pas en effet un certain détachement du réel[13], et ne marque-t-il pas ainsi "l'envol même de la pensée"? Il s'agit en fait d'une systématisation de la pensée opératoire, de telle sorte qu'elle ne soit plus contrainte de se subordonner à la manipulation concrète. La mise en rapport de différentes propositions (au sens logique), reçues comme de simples hypothèses, va permettre de structurer un champ des possibles et d'en déduire le réel, au lieu d'induire, comme auparavant, ce qui peut être de ce qui est. C'est ainsi, comme nous le verrons bientôt, que s'affirme une véritable pensée expérimentale utilisant un raisonnement "hypothético-déductif". Un grand nombre de difficultés rencontrées par les adolescents semblent avoir pour cause l'abord délicat de cet opératoire formel ; cf. l'analyse d'une expérience de soutien à Antony[14], qui relevait, parmi les plus nombreux échecs : conjecturer, déduire, conclure, trouver des hypothèses, trouver une partition... Même si de nombreux troubles s'enracinent dans l'opératoire concret (classer, hiérarchiser, ordre chronologique, etc...), l'examen de cet abord de l'opératoire formel est donc au coeur de notre sujet.

Le groupe I.N.R.C.

Comment s'opère cette refonte systématique de la pensée opératoire? Par la synthèse des deux formes de réversibilité, réversibilité par annulation ou inversion, et réversibilité par réciprocité ou compensation. Nous avons déjà rencontré, sans le savoir, ces deux formes de réversibilité dans l'expérience des deux verres ; en effet, pour comprendre immédiatement que le contenu du verre haut et mince est bien identique au contenu du verre bas et large - et cela sans en rester à la "renversabilité" - il faut déjà mettre en jeu un subtil mécanisme, qui rapporte, grâce à la réversibilité par annulation ou inversion, le haut et le bas d'une part, le mince et le large d'autre part ; cela seul permet alors de comprendre la réversibilité par compensation ou réciprocité entre "+ mince" et "+ haut", pour ensuite pouvoir immédiatement affirmer que la quantité à boire est bien identique dans les deux verres. La réversibilité par annulation ou inversion a lieu dans le registre des éléments : soit l'opération "I" consistant à ajouter un élément
x à A, [ I(A) = (A + x) ], elle peut être coordonnée avec l'opération inverse (soit, par exemple, l'opération "N") qui consiste à retrancher l'élément x. Ainsi, à partir de (A+x)=B, on aurait alors
N(B) = N( I(A) ) = N(A+x) = (A+x) - x = A .
L'opération I est donc bien ici réversible par annulation ou inversion. La réversibilité par compensation ou réciprocité a par contre lieu dans le registre des relations : soit la relation I, "plus grand que", ou "strictement supérieur …", notée />/, dans un ensemble d'entiers naturels donnés, I(x)=y signifierait donc x>y. Cette relation peut-être coordonnée avec la relation réciproque, soit par exemple l'opération R notée /</, telle que, à partir de notre y précédent, nous ayons : R(y) = R( I(x) ) = x . L'opération I est bien ici réversible par réciprocité ou compensation, en étant coordonnée avec l'opération R.

Un exemple rendra plus claire la présentation de ces deux formes de réversibilité. Prenons, à la suite de Piaget[15], une balance romaine en équilibre. Notre opération « I » pourrait ici consister à poser un poids "p" sur le plateau de cette balance. L'opération inverse, soit N, négation de l'opération I, grâce à laquelle nous concevons I comme réversible par inversion ou annulation consisterait alors à retirer un poids "p" de ce plateau. En partant de l'état final de l'opération I, la balance se retrouverait ainsi en équilibre, nous aurions annulé l'opération I. Il est également possible d'annuler l'effet de l'opération I sans agir pour autant sur l'élément "p". Il faut alors agir sur la relation entre le poids "p" d'une part et, d'autre part, la force résultant du produit entre le poids de référence accroché au fléau et la distance de ce poids par rapport à « l'axe » de la balance romaine. C'est d'ailleurs ainsi que se réalise une pesée à l'aide de ce type de balance. En augmentant la distance entre le poids de référence et l'axe, on augmente le produit de cette distance et du poids, c'est à dire le "moment" (au sens physique) déterminant la force qui s'applique sur l'axe. On peut alors rétablir l'équilibre en agissant non pas au niveau des éléments, puisque notre poids "p" reste posé sur le plateau, mais au niveau des relations en modifiant la distance du poids de référence à l'axe. Nous aurions ainsi notre opération R, réciproque de l'opération I, qui restaurerait l'équilibre sans agir sur les éléments. A titre d'indication pédagogique, signalons que l'utilisation d'une balance Roberval n'éclaircit nullement l'exemple donné. En effet, soit nous ne disposons pas d'une balance dont la distance des plateaux à l'axe n'est pas réglable. En ce cas, la négation de I par compensation ou réciprocité consisterait à ajouter un même poids "p" sur l'autre plateau pour retrouver l'équilibre. Mais il est gênant que la négation par réciprocité s'effectue ici à l'aide d'une opération de nature semblable à l'opération I, alors qu'elles doivent être différentes. Soit, nous disposons d'une balance dont la distance des plateaux à l'axe est réglable, et nous pourrions alors espérer retrouver deux opérations, R et I, bien distinctes, l'une jouant sur la distance, l'autre ajoutant un poids. Mais hélas il y a là une triple manière de mettre en évidence la réversibilité de l'opération I par réciprocité ; on peut en effet, ou bien ne pas modifier la distance et agir comme précédemment, ou bien (si le poids "p" n'est pas trop important) augmenter la distance de l'autre plateau à l'axe, ou bien encore réduire la distance du premier plateau à l'axe, tout cela ne simplifiant pas la tâche des élèves.

Jusqu'à présent, nous n'avons fait que présenter séparément les deux formes de réversibilité. Or, puisqu'il doit s'agir, à l'opératoire formel, d'une systématisation de la pensée opératoire, il nous faut tenter d'expliquer en quoi ces deux formes se trouvent elles-mêmes coordonnées. Nous effectuerons cela en deux temps, en commentant d'abord un exemple de Piaget, puis, dans le paragraphe suivant, en traduisant un autre exemple de Piaget en termes de logique formelle, de manière à introduire notre critique des conceptions piagétiennes. L'exemple qui nous servira tout d'abord à préfigurer la coordination des deux formes de réversibilité illustre l'émergence de la pensée expérimentale. On présente à l'enfant[16] des tiges métalliques fixées perpendiculairement à un support vertical. Ces tiges diffèrent par la longueur, l'épaisseur, la forme de la section, et la matière. Il s'agit de déterminer les causes de leurs différentes flexibilité. Avant la maîtrise de l'opératoire formel, pour démontrer l'efficience de la longueur, il arrive encore qu'un enfant de 11/12 ans compare une tige longue et mince avec une tige courte et épaisse, "pour qu'on voit mieux la différence"[17]. La réversibilité par inversion ou annulation semble bien ici comprise, puisque les tiges comparées seront opposées ou bien par la longueur, ou bien par l'épaisseur, la qualité de l'une s'opposant alors à la même qualité chez l'autre. La réversibilité par réciprocité ou compensation semble également acquise, puisque l'enfant ne compare pas une tige longue et épaisse avec une tige courte et mince, mais une tige longue et mince avec une tige courte et épaisse. Il a donc bien saisi, en un sens, que l'épaisseur, qualité différente de la longueur, pouvait annuler les effets de cette dernière sans que l'on modifie la longueur elle-même. Ce qui manque encore à l'enfant interrogé est donc la synthèse des deux formes de réversibilité, en comprenant qu'il est inutile – et, dans ce cas, nuisible – d'agir sur les deux à la fois puisque la réversibilité par réciprocité produira exactement le même effet que la réversibilité par inversion. En cumulant les deux, l'enfant témoigne qu'il n'a pas tout à fait compris cela, bien que, en comparant une tige longue et mince avec une tige courte et épaisse, il ait commis là une "bonne faute", indice de sa compréhension à venir. Nous reviendrons, dans un développement ultérieur, sur cette question qui représente le point d'ancrage de toutes les pédagogies de l'erreur et de l'évaluation formative dans la psychologie cognitive. Grâce à la claire compréhension de la synthèse des deux formes de réversibilité, nous pouvons maintenant saisir ce qui arrive au pauvre escargot[18] avançant sur une planchette elle-même mobile par rapport à une table. Par l'opération I, l'escargot avance sur la planchette ; l'opération N, négation par annulation ou inversion de l'opération I, consisterait à reculer sur la planchette ; l'opération R, réciproque de l'opération I, consisterait à avancer la planchette sans que l'escargot avance ; et l'opération C, négation par inversion ou annulation de l'opération R, est également la réversible de l'opération I par compensation ou réciprocité ; elle nous permet de retrouver l'escargot demeurant, malgré tout ses efforts, par rapport à la planchette, dans la même position qu'après l'application de l'opération N. Avant de comprendre que l'opération C se révèle ainsi être la réciproque de l'opération N, notons simplement que nous sommes maintenant en possession de l'intégralité du groupe I.N.R.C : I désignant l'opération de départ ou "identique", N désignant sa négation, R désignant sa réciproque et C sa corrélative, toujours ici à propos de l'opération initiale I.

Traduction du groupe INRC en logique formelle.

La traduction du groupe INRC en termes de logique formelle est indispensable à notre intervention, puisque c'est en récusant l'importance accordée à ce formalisme que nous critiquerons les analyses de Piaget. Ce passage par le formalisme correspond à la démarche de Piaget lui-même. En effet, l'accès au raisonnement hypothético-déductif requiert la capacité de comparer entre elles de pures hypothèses afin d'en dégager un schéma possible d'interprétation - une théorie - que l'expérience mettra à l'épreuve du réel. Ces pures hypothèses revêtent l'aspect de propositions logiques, c'est à dire d'énoncés pouvant être vrais ou faux. Dans la mesure où il s'agit de les combiner tout en restant dans le champ des purs possibles, c'est moins à leur contenu qu'à la forme de leur combinaison qu'il va falloir prêter attention. Nous devons donc distinguer la vérité d'une proposition, concernant son contenu, de la validité d'un raisonnement, concernant sa forme. Nous pénétrons alors dans le domaine de la logique formelle, et c'est ainsi qu'un raisonnement du type "si 2 + 2 = 4, alors Londres est la capitale de l'Angleterre" est admis comme valide, bien que le contenu des deux propositions ci-dessus ne permette pas d'établir un rapport entre elles. Le maniement du groupe INRC nous engage donc à considérer les seize opérations binaires dans la combinatoire élémentaire d'une logique bivalente, c'est à dire d'une logique qui n'admet que deux valeurs de vérité : vrai et faux. Ces opérations sont dites binaires car elles concernent la combinaison de deux propositions, et il y en a 16 puisque, à partir de la combinaison des 2 valeurs de vérité que peuvent avoir chacune des deux propositions
[ (VV), (VF), (FV), (FF) ], nous obtenons 16 types (4 fois 4) de résultats possibles pour l'ensemble des quatre valeurs de vérité que l'on attribue à chaque combinaison binaire. Nous ne retiendrons ici, pour la nécessité de l'exposé, que trois des seize opérations binaires fondamentales : celles des opérateurs /^/, correspondant à "et", /v/ correspondant à notre "ou" inclusif (l'un ou l'autre, ou les deux), et / => /, l'implication, exprimable sous la forme "si... alors...". Gardons en mémoire les tables de vérité de ces opérations :

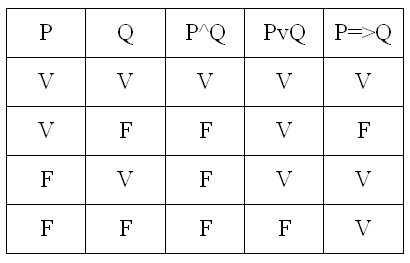
Nous aurons également besoin - des "lois de Morgan", selon lesquelles, Øp désignant la négation de p, nous avons :

Ø(pvq) <=> Øp ^ Øq

et

Ø (p^q) <=> Øp v Øq.

ainsi que l'équivalence :

(p => q) <=> Øp v q.

Bien que ces signes et ces lois paraissent abstraits et inutiles, nous les employons quotidiennement, ainsi que le fait remarquer l'épistémologue R. Blanché dans Introduction à la logique contemporaine[19]. Reprenons son exemple qui nous servira d'entraînement au maniement de ces signes ; nous admettons l'équivalence des deux phrases : "s'il me rencontre, il me salue toujours", et, "il ne me rencontre jamais sans me saluer". Démontrons cette équivalence à l'aide de la logique ; soit r = "il me rencontre" et s = "il me salue". "S'il me rencontre, il me salue toujours" devient (r => s), et "il ne me rencontre jamais sans me saluer" devient « Ø (r ^ Ø s) ». Or, nous savons que
(p => q) <=> (Øp v q), et, en appliquant les lois de Morgan
à Ø (r^Øs), nous retrouvons bien (Ør v s), c'est à dire (r => s).

Nous sommes maintenant capables de comprendre un exemple simple de l'application du groupe INRC à la pensée expérimentale, ainsi que sa traduction en logique formelle. Je me trouve devant un phénomène dont je cherche à découvrir la loi : une lumière s'allume et, simultanément, un mobile s'arrête[20]. La première hypothèse nous donnera l'opération I : la lumière cause l'arrêt du mobile, soit, avec p = lumière et q = arrêt : (p =>q). Il nous faut rechercher un contre-exemple pour vérifier notre hypothèse, ce contre-exemple serait l'existence de la lumière sans qu'il y ait arrêt du mobile, soit (p^Øq). Or, nous avons bien (p =>q) <=> (Øp v q) et, en niant cette dernière proposition :
Ø (Øp v q) <=> (ØØp ^ Øq) <=> (p^Øq),
ce qui nous donne notre contre-exemple, qui désignera donc l'opération N. Mais on peut également décrire le même effet (l'allumage de la lumière qui se produit simultanément à l'arrêt du mobile) en partant d'une autre hypothèse, ce qui nous donnera l'opération R. L'arrêt du mobile pourrait en effet provoquer l'allumage de la lumière. Nous aurions alors (q => p) avec comme contre-exemple l'existence d'un arrêt sans allumage : (q^Øp). En appliquant les mêmes lois que précédemment, on vérifie que
(q ^ Øp) constitue bien la négation de (q => p) :
(q ^ Øp) équivaut en effet, en appliquant à rebours les lois de Morgan, à Ø (Øq v p), ce qui nous donne bien,
puisque (Øq v p) <=> (q => p), la négation de (q => p).
Nous avons donc ici la négation de l'opération R, ce qui définit l'opération C, c'est à dire la corrélative de notre opération I ci-dessus.

Avant d'aborder la présentation du cas "Roc.", il nous faut dire un dernier mot pour souligner l'enthousiasme de Piaget face à ce qu'il appelle[21] la "beauté" de ce système, et nous comprendrons ainsi pourquoi l'on peut qualifier l'ensemble des opérations INRC de groupe, au sens mathématique. Nous signalions, à propos du pauvre escargot, que l'opération C nous permettait de le retrouver dans le même état que l'opération N, bien qu'elles soient toutes deux différentes. Cela signifie que C se présente comme la réciproque de N, puisque la relation réciproque consiste à obtenir le même effet en appliquant une autre opération. Traduisons cela en termes de relations ; avec les majuscules désignant des fonctions et les minuscules le résultat des opérations, nous avons :
I(i) = i ; N(i) = n ; R(i) = r et C(i) = c. L'opération C se présentant comme la réciproque de l'opération N, il faudrait écrire, puisqu'il s'agit d'opérer sur les opérations elles-mêmes,
R(N(i)) = C(i), ce que l'on retrouve dans les ouvrages de Piaget sous la forme RN = C. Il serait tout à fait possible de traduire cela en logique formelle, à l'aide de l'exemple précédent, en sachant que l'on obtient la réciproque par la transformation de l'opérateur /^/ en opérateur /v/, ou vice versa, après avoir nié la proposition initiale. Mais ce n'est pas seulement la réciproque de la négation qui donne la corrélative, ce sont n'importe lesquelles des opérations - à l'exception de l'opération I jouant le rôle de l'élément neutre - qui, combinées deux à deux, nous donnent la troisième. C'est cela qui permet à Piaget de retrouver la structure mathématique du groupe de Klein, remarquable par ses symétries :

Voilà la beauté formelle du système...

LE CAS "ROC.".

La compréhension des inclusions.

L'examen du cas de "Roc." se situe dans le cadre de la compréhension des inclusions, et plus précisément de la complémentarité de celles-ci, au stade opératoire formel. Ainsi que le présente Piaget dans la Genèse des structures logiques élémentaires[22], on pourrait s'attendre, chez des enfants abordant l'opératoire formel, non seulement à ce qu'ils maîtrisent le relation d'inclusion, ce qui est un pré-requis, mais encore à ce qu'ils comprennent l'équivalence entre l'inclusion d'une classe A dans une classe B et l'inclusion de la classe complémentaire "ØA" dans la classe complémentaire "ØB", soit (A Ì B) <=> (ØB Ì ØA). Cela pourrait ne constituer qu'une simple application du groupe INRC, puisque nous retrouvons coordonnées dans cette équivalence[23] l'inversion (A/ØA ; B/ØB) et la réciprocité (dans le double usage de la relation d'inclusion). Interrogeant des enfants de 10 à 13 ans en amenant progressivement la question "y a-t-il plus d'êtres vivants qui ne sont pas oiseaux ou pas animaux?", Piaget est conduit à répartir son échantillon en quatre groupes : " (1) ceux qui échouent aux questions (A<B) et (non-B < non-A) ; (2) ceux qui réussissent aux premières et échouent aux secondes ; (3) ceux qui réussissent aux premières et parviennent à résoudre les secondes, mais après de nombreux tâtonnements ; et (4) ceux qui réussissent sans difficultés aux secondes comme aux premières."[24]. Tentez de poser la question piagétienne à un groupe d'adultes diplômés, vous comprendrez pourquoi notre principal problème devient maintenant de comprendre sur quoi Piaget peut bien se fonder pour attendre une réponse immédiate...

Il nous faut d'abord souligner que, comme beaucoup de "pré-requis", la compréhension de l'inclusion simple n'est pas sans présenter de nombreuses difficultés. Si cette compréhension peut, comme nous le verrons dans le paragraphe suivant, être exprimée avec le groupe INRC, sa maîtrise n'exige pourtant que des capacités ressortissant à l'opératoire concret. Il s'agit en effet de bien comprendre que, B étant différent de A, "A est inclus dans B" ne veut nullement dire que tous les éléments de B sont des éléments de A. Quelles sortes de problèmes peuvent alors se poser? Ecoutons les réponses de quelques enfants appartenant aux groupes (1) et (2) : "<groupe 1> Y a-t-il plus d'animaux ou plus d'oiseaux ? - Les oiseaux sont des animaux, c'est la même chose. (...) Et y a-t-il plus de canards ou plus d'oiseaux? - Les canards font partie des oiseaux, les canards sont des oiseaux aussi.- Et quand en a-t-on le plus, quand on compte seulement les canards ou quand on compte les oiseaux? - C'est la même chose, puisque les canards sont des oiseaux. - Il y a combien de canards? - (il les compte) Quatre. - Et d'oiseaux? - Huit. - Y a-t-il plus de canards ou plus d'oiseaux? - C'est la même chose. " <groupe 2> : " Si un chasseur voulait tuer tous les canards, et un autre tous les oiseaux, est-ce qu'il resterait plus après avoir tuer tous les canards ou tous les oiseaux? - Plus quand je tue tous les oiseaux... Y a-t-il plus d'êtres vivants qui ne sont pas des oiseaux ou plus qui ne sont pas des animaux? - La même chose, rien."[25]. Dans un cas comme dans l'autre - bien que la question portant sur non-B inclus dans non-A soit plus abstraite - on peut rapidement indiquer que le noeud de la difficulté réside dans une maÎtrise insuffisante de la réversibilité des rapports entre la partie et le tout. Il s'agit d'une forme simple de réversibilité, qui consiste à appréhender la partie comme étant à la fois un tout, lorsqu'on la considère en elle-même, et partie d'un tout plus grand lorsque l'on considère en même temps ce plus grand tout et la partie comme telle. A défaut, on se retrouve systématiquement devant des problèmes de ce type : face à dix billes dont sept blanches et trois noires (ou tant de primevères et tant de fleurs, tant de canards et tant d'animaux, etc...), l'enfant sachant compter les billes, disant qu'il y a plus de billes blanches que de billes noires, répondra quand même qu'il y a plus de billes blanches que de billes.

En transposant cela dans le formalisme INRC, l'enjeu consiste à poser à la fois I et C, la relation d'inclusion de A dans B d'une part, et d'autre part le fait qu'il y ait des éléments de B (soit "b") qui ne soient pas pour autant des éléments de A (soit "a"). La transcription formelle de "A inclus dans B" devient "a => b", dans le sens de "si a est élément de A, alors a est élément de B". Nous avons alors, avec une notation simplifiée :
I = (a =>b) ; N = Ø (a =>b) = Ø (Øa v b) = (a ^ Øb) ;
R (obtenue en niant I puis en inversant l'opérateur) = (a v Øb) ;
et C = NR = Ø (a v Øb) = (Øa ^ b), cette corrélative signifiant donc bien qu'il y a des éléments de B qui ne sont pas des éléments de A.

La comprehension formelle des inclusions complementaires.

Les enfants des groupes 3 et 4 surmontent une difficulté plus grande, puisqu'il s'agit non seulement de penser l'inclusion simple, mais encore de la penser en même temps que l'inclusion réciproque des classes complémentaires. La notion de classe complémentaire engageant une réversibilité par inversion ou annulation, il doit bien y avoir ici synthèse des deux formes de réversibilité. C'est dans cette mesure que la question posée est une application du groupe INRC. En effet, nous avions, avec A inclus dans B :
I = (a =>b) ; N = (a ^ Øb)  ; R = (a v Øb) ;
et C = NR = Ø (a v Øb) = (Øa ^ b). Nous retrouvons maintenant, avec non-B inclus dans non-A :
I' = (b =>a) ; N' = (Øb v a) = (b ^ Øa) ; R' = (b v Øa) ;
et C'= N'R' = Ø (b v Øa) = (Øb ^ a).
La liaison de I' avec C' étant toujours nécessaire, comme dans le cas précédent, pour penser convenablement l'inclusion.

Il est bien clair, l'opérateur /^/ étant commutatif [(p^q) <=> (q^p)], que la transcription formelle de la corrélative C'(Øb ^ a) nous donne une proposition exactement équivalente à la corrélative C (Øa ^ b). La nécessité, apparue dans la transcription formelle de la compréhension de l'inclusion simple, de penser ensemble l'identique et la corrélative implique donc que l'on ne pourrait, en principe, comprendre les deux inclusions simples
(A Ì B) et (ØB Ì ØA) sans comprendre immédiatement leur équivalence. En effet, d'un point de vue formel, cette équivalence saute aux yeux dès que l'on pose les deux corrélatives C et C'. Mais cette équivalence ne se produit immédiatement que du point de vue du formalisme ; il nous resterait à comprendre si ce point de vue est ou non celui de "Roc.", élève en difficulté...

Les difficultes de "roc.".

"Roc." est en effet situé dans le groupe 3, groupe, rappelons-le, qui réussit aux questions "A est inclus dans B", mais ne parvient à résoudre celles du type "non B inclus dans non A" qu'après "de nombreux tâtonnements". Il faut souligner que ces tâtonnements en question vont être immédiatement assimilés par Piaget à des difficultés qu'éprouve l'enfant ; ce qui apparaît en relisant la présentation du groupe 4 : "ceux qui réussissent sans difficultés aux secondes comme aux premières". Une lecture pédagogique de cette expérience de Piaget commande deux questions fondamentales. Premièrement : est-il légitime de confondre ainsi tâtonnement et difficulté? Deuxièmement, question sur laquelle nous reviendrons dans notre deuxième partie : une réponse immédiate peut-elle être l'indice d'une compréhension? D'autant qu'il se pourrait fort, à bien lire les réponses de Roc, que celui-ci n'éprouve de réelles difficultés qu'en répondant aux questions de Piaget, mais non pas en cherchant à résoudre le problème lui-même, indépendamment de - ou plutôt ici, malgré - la manière dont il est présenté.

Voici la transcription complète des réponses de Roc, 11 ans et 7 mois : "Y a-t-il plus de canards ou plus d'oiseaux? - Plus d'oiseaux parce que les canards sont des oiseaux. - Et plus d'animaux ou plus d'oiseaux? - Plus d'animaux parce que les oiseaux sont des animaux. - Et dans le monde? - Plus d'animaux parce que les oiseaux sont des animaux.

Y a-t-il plus d'êtres vivants qui ne sont pas des canards ou plus qui ne sont pas des oiseaux? - (Hésite) Plus de pas oiseaux... ça se vaut. - Et si un chasseur tue tous les canards et un autre tous les oiseaux (etc...)? - Il y a plus de pas canards, parce qu'il y a tous les oiseaux qui ne sont pas des canards plus les animaux qui ne volent pas. - Et plus... pas oiseaux ou pas animaux? - Il y a plus d'êtres vivants qui ne sont pas des oiseaux, parce qu'il y a tous les animaux qui ne volent pas. Les pas animaux ne sont même pas des oiseaux : ils ne sont rien. Les pas oiseaux, il reste tous les animaux qui ne volent pas. - Et dans le monde? - (Hésite) Il y a plus de pas oiseaux. - Pourquoi? - Il reste les animaux qui ne volent pas et les êtres humains"[26].

Il est bien clair que Roc a des difficultés à répondre aux questions de Piaget. Mais il apparaît aussi qu'en tâtonnant, Roc arrive à résoudre les difficultés qui se présentent pour répondre au problème lui-même, ou du moins à sa propre formulation du problème. Pour mieux comprendre cela, il nous faut quitter un moment le formalisme piagétien et tenter une autre lecture des réponses de Roc.

CRITIQUE DU FORMALISME PIAGÉTIEN.

De nouveaux instruments conceptuels.

On peut en effet interpréter le problème posé sans se servir du langage formel accompagnant le groupe INRC. Il suffit de s'en tenir à une représentation ensembliste des inclusions, en utilisant, pour décrire l'activité intellectuelle en question, non plus le langage logique mais des catégories empruntées à la psychologie de la forme, celles de figure et de fond. Rappelons que, pour la psychologie de la forme ou Gestalttheorie, toute perception d'objet, par exemple dans la vision, a pour condition la perception de différences entre cet objet et le reste du champ visuel, différences surtout d'intensité ou de contraste. Ce qui veut dire que :"Tout objet sensible n'existe donc qu'en relation avec un certain "fond" ; cette expression s'applique non seulement aux choses visibles, mais à toute espèce d'objet ou de fait sensible ; un son se détache sur un fond constitué par d'autres sons ou bruits ou sur un fond de silence, comme un objet sur un fond lumineux ou obscur"[27]. L'objet perçu, qui servira de matière à l'activité intellectuelle, se présente donc toujours comme figure se détachant sur un fond. La mise en évidence de ce rapport figure/fond est très sensible dans les exemples des figures ambiguës, où l'on voit alternativement une figure se détachant sur un fond, puis ce fond lui-même devient une nouvelle figure se détachant sur fond de l'ancienne figure que l'on ne perçoit donc plus comme telle. Ainsi :

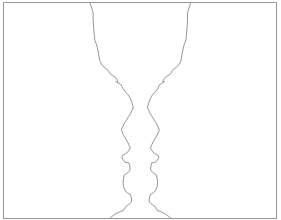
Une lecture gestaltiste du problème.

En utilisant ces catégories nous pouvons revenir vers le problème posé. Soit tout d'abord l'inclusion simple de A dans B :  

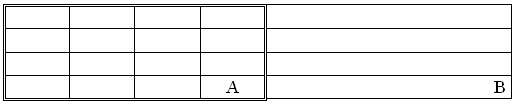
Il est clair que nous commençons par saisir A comme figure sur fond de B. Pour bien comprendre cette inclusion, il est aussi nécessaire de comprendre, A et B étant distincts, qu'il y a des éléments de B qui ne sont pas des éléments de A. Il nous faut alors percevoir (non A), = (B-A), comme figure sur fond de B.

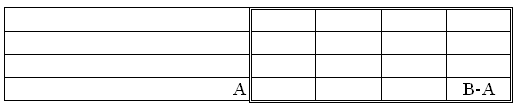
Ce détachement de non-A sur fond de B correspond à la corrélative C = (a ^ b) qu'il fallait saisir pour bien comprendre l'inclusion I = (a =>b).

Que se passe-t-il maintenant avec l'inclusion complémentaire non-B inclus dans non-A? Demandons nous simplement : comment est-il possible de se représenter cela à l'aide des diagrammes précédents? Il y a une véritable difficulté ; comment en effet se représenter non-B? Cela n'est possible qu'à condition d'imaginer un troisième ensemble, soit E, tel que A  B  E. Nous aurions ainsi :

Ou plutôt, afin de mieux faire ressortir non-A et non-B que l'on doit ici comparer :

Comprendre alors que non-B est inclus dans non-A revient, dans un premier temps, à détacher non-B (= E-B) sur fond de non-A (= E-A). Et, dans un second temps, bien comprendre l'inclusion de non-B dans non-A implique de saisir qu'il existe des éléments de non-A qui ne sont pas des éléments de non-B. Il faut alors détacher (non-A - non-B) sur fond de non-A. Il est évident que si l'on ne présuppose pas E, non-B étant vide, il est impossible de se représenter le détachement de (non-A - non-B) figure sur non-A fond. La position de E est donc bien une condition indispensable à la résolution du problème.

Poursuivons : ce détachement de (non-A - non-B) sur fond de non-A est ce qui permet de bien comprendre l'inclusion de non-B dans non-A, en ne la confondant pas avec une simple identité de non-B et de non-A. C'est à dire que, tout comme pour A inclus dans B où le détachement de (B-A) correspondait à la corrélative
C = (Øa ^ b), le détachement de (non-A - non-B) sur fond de non-A correspond ici à la corrélative C' = (b ^ Øa),corrélative C' que l'on doit nécessairement penser en même temps que I' = (Øb => Øa) pour bien comprendre l'inclusion complémentaire. Mais alors, qu'en est-il de la raison qui permettait d'attendre la compréhension immédiate de l'équivalence entre A inclus dans B et non-B inclus dans non-A? Manifestement, si nous avions auparavant une équivalence immédiate entre les corrélatives C et C', on ne peut plus du tout parler maintenant d'une même activité intellectuelle pour le détachement de (B-A) sur fond de B et le détachement de (non-A - non-B) sur fond de non-A. Il n'y aurait alors plus lieu de s'attendre à une réponse immédiate, à une "compréhension complète dès la question posée"[28]. Que deviennent alors les difficultés de Roc?

Le parcours de Roc.

Nous pensons que ce mode d'approche du problème, le traduisant en langage ensembliste et non plus en logique des propositions, est exactement celui de Roc. En effet, la première hésitation de Roc, lors du passage de ({canards} Ì {oiseaux}) à ({non-canards} Ì {non-oiseaux}), trahit une difficulté à penser la classe complémentaire, alors même que l'ensemble des animaux est déjà pensé dans la première série de questions. Cette difficulté se renforce lorsqu'il s'agit de se représenter la classe complémentaire des non-animaux. Roc ressent ici la même difficulté que nous éprouvions tout à l'heure lorsqu'il fallait nous représenter non-B inclus dans non-A à l'aide des seuls ensembles A et B. "Les pas animaux ne sont même pas des oiseaux : ils ne sont rien". Or, c'est avec un "matériel d'images d'animaux"[29], probablement semblable à celui représenté p. 114, que Piaget interroge Roc. Le fait est qu'il n'y a là que des images d'animaux. Malgré tout, Roc tente - et c'est cela qu'expriment ses tâtonnements - de constituer une classe analogue à notre ensemble E. C'est ainsi que la réponse finale "il y a plus de pas oiseaux", est justifiée par "il  reste les animaux qui ne volent pas et les êtres humains". En ajoutant les êtres humains, Roc se donne lui-même, constituant par là une classe analogue à notre ensemble E, le matériel dont il ne dispose pas et qui lui est pourtant nécessaire pour résoudre le problème posé.

Certes, si tant est que l'opératoire formel doive être accessible à tous, cela n'invalide pas les conclusions de Piaget puisque Roc avait encore besoin d'un matériel imaginaire pour penser. Sans nous demander ici si la pensée sans image est encore une pensée, tirons immédiatement quelques conclusions pédagogiques. La difficulté ressentie par Roc et qui permettait à Piaget de le situer dans le groupe des enfants (adolescents ?) en difficulté face à l'opératoire formel, cette difficulté provient d'abord du matériel proposé qui ne rend pas possible la représentation d'un ensemble englobant celui des animaux. La situation de Roc dans le groupe des enfants en difficulté pourrait alors relever d'un "malentendu pédagogique"[30], ici au sens où l'évaluation de Roc serait faussée par l'inadéquation du matériel à la tâche proposée, ou, plus exactement, au parcours, à la stratégie de résolution que l'élève est à même de mener à bien. Nous laisserons pour l'instant de côté la question de savoir si ce malentendu pédagogique n'est pas aussi un malentendu pour le psychologue à qui ferait défaut une attitude pédagogique authentique. Toujours est-il que la difficulté prise en ce sens serait à distinguer radicalement des tâtonnements qui, au contraire, expriment la capacité de Roc à poursuivre son parcours jusqu'à la solution du problème. Une pareille confusion entre tâtonnement et difficulté a de bien fâcheuses conséquences et doit, dans la plupart des cas, entraîner l'échec, à cause d'un défaut d'attention au parcours de l'élève. L'attitude pédagogique, que nous aborderons dans notre Deuxième Partie, consisterait nous semble-t-il à faire la part entre tâtonnements et difficultés pour transformer la situation d'acquisition des connaissances en fournissant un matériau à ces tâtonnements. Il est vrai que les tâtonnements peuvent ne pas être guidés par l'invention ou l'appréhension d'un parcours, et traduire ainsi de très réelles difficultés. En ce cas, il appartient certainement aussi au pédagogue de rendre alors cette appréhension possible.

---